

Praneeth Reddy Sudalagunta
Data Scientist. Cancer Researcher. Aerospace Engineer.
Optimal Aero-assisted Orbital Transfer with Predictive Time-linear Control
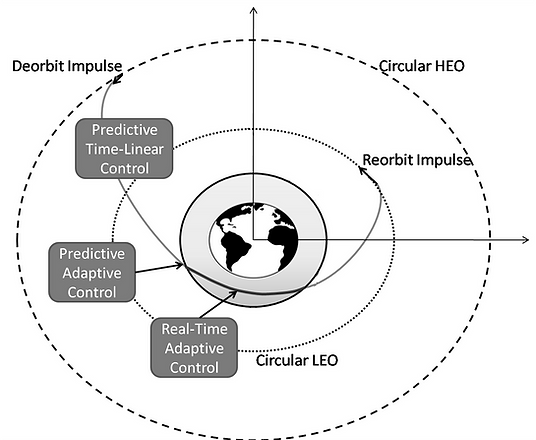
Spacecraft Trajectory Optimization Strategy using an Aero-assisted Orbital Transfer Maneuver.
In the realm of spacecraft dynamics and control, inter-orbital transfer capability has a potential of saving billions of dollars. Relaunching new satellites every time a major technological advancement is made, is not ideal from an economic and space environmental point of view. Instead, we would prefer launching a technology-refurbishing mission equipped with electromechanical devices capable of replacing the outdated hardware with the latest one. However, it is desirable
that this space vehicle responsible for replenishing technological capabilities be parked on a low earth orbit (LEO) for easy access. Hence, we require spacecrafts from higher orbits to descend into this parking orbit for a hardware upgrade.
Early efforts towards achieving orbital transfer included using a propulsive maneuver where the thrust of the spacecraft is used to change the direction and magnitude of its velocity vector. In reality, the thrust applied is only for a very brief period of time. Hence, it can be considered as an impulse. Orbital transfer can be implemented to achieve a change in angle of inclination, eccentricity and distance from periapsis of a spacecraft in a given orbit. If the initial and the desired final orbits intersect with each other, it is possible to execute a Hohmann transfer using only one impulse. Otherwise, one would require at least two impulses to carry out the maneuver, where the fi rst one is called the de-orbit impulse and the second one is called the re-orbit impulse. Aeroassisted orbital transfer (AOT) originated from the idea of using the de-orbit impulse to dip a spacecraft into a planet's atmosphere and use the atmospheric forces to achieve the desired conditions at the exit so as to collectively reduce the expenditure involved in executing a conventional two-impulse transfer. As expected, a typical spacecraft cannot sustain the aerothermodynamic loads involved during re-entry. At the same time, a re-entry vehicle is designed to sustain much higher loads than that experienced during an AOT maneuver which clearly indicates that AOT maneuver requires a specially designed vehicle called an aeroassisted orbital transfer Vehicle.it is observed that an optimal control law derived to execute such a maneuver, in the absence of additional constraints, often assumes a linear function in time. Optimal time-linear control laws are easy to implement and the fact that they minimize a certain cost function, only makes them more desirable.
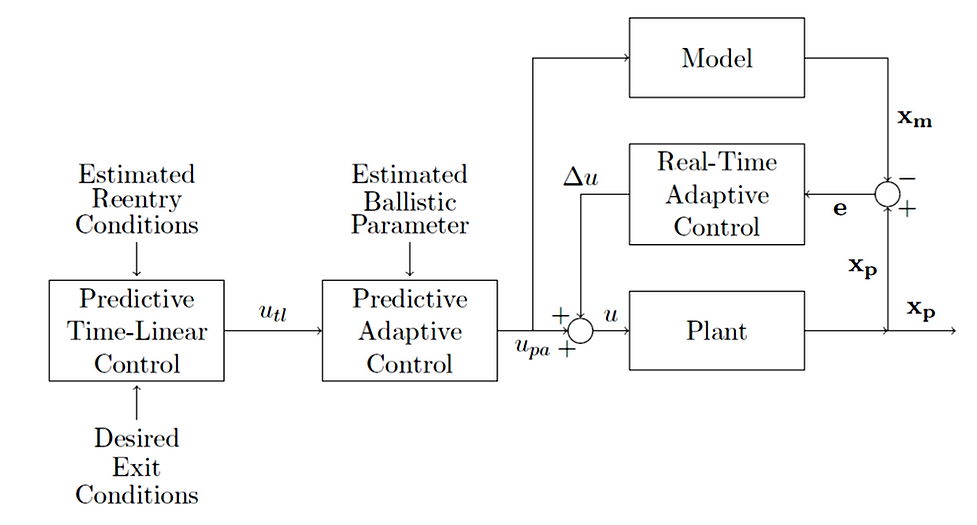
An overview of the proposed scheme to control an aero-assisted orbital vehicle featuring feed-forward and feedback loops.
The present work develops a novel scheme that is used to obtain optimal time-linear control laws by predicting the time required by the minimization problem to yield a time-linear control law. This is accomplished by nondimensionalizing time with respect to the terminal time and solving for the two-point boundary value problem with terminal time as a parameter. As a result the spacecraft may spend a longer or a shorter time inside the atmosphere. However, the resulting control law is linear in time and optimal.

